If you’ve read my about page, you know I have some ill-defined ambitions to eventually create a proprietary trading firm. This is probably a five to ten years out kind of thing, so there are essentially no details around the idea. Just some broad philosophies, a few lessons learned from the failures of other firms, and a belief that trading in groups is better than trading alone. But there’s one thing about this hypothetical firm that I have already decided – what poster I’ll have on my office wall. I’m going to have to have it custom made, but that’s OK. It’ll be worth it. The picture will be the rather nerdy looking Bell Labs engineer you see at right – John L. Kelly. The text on the poster will be:
Maximize The Expected Value Of The Logarithm Of Your Wealth. Then reduce your bet size by a factor of 5.
If I were competent at Photoshop I’d create a mock up of the poster. But since I’m not, you’ll just have to imagine it. This statement is incredibly dense – you could legitimately write a small book explaining what it means and why it’s a good idea. I’m not going to go that in depth, but there is enough material that I’ve decided to split it into parts to keep the post length reasonable. Today I’m going to look at the maximizing aspect.
If you’re reading this blog, it’s pretty certain you want to maximize your wealth. I’m also going to assume you have some amount of wealth separated out as risk capital – money with which you can take investing or speculative bets. The question then becomes what bets to take to maximize your wealth. Expectation math (explained here) offers a partial answer. But it turns out to be a very incomplete way of thinking. To illustrate why that is, here’s a little thought experiement.
Suppose you had exactly $100 to your name. You meet a man who offers you a bet: he will flip a fair coin. If it comes up heads, he will give you $2. If it comes up tails, you must give him $1. Better yet, the bet size can be scaled: you can decide how big you want the wins and losses to be – for example you could choose to win $4/lose $2 instead of $2/$1. You can scale the size of the bet up or down by any multiple you like. But wait, there’s more: the man will continue to bet with you as long as you like, and you can re-scale the bet size each time. As long as you keep betting, he’ll take the other side. But if you stop, he’s done. We’ll assume the man has plenty of money to cover his losses.
The question is how much you should bet on the first bet? How does it change on subsequent bets?
Now, let’s think about this bet a little. We’ve clearly gotten VERY lucky. We’re almost broke and yet we’ve stumbled on this man has the potential to make us rich. Suppose we just bet $1 with him repeatedly. Expectation math says that we’d on average make $0.50 per bet. Not bad – do this say a hundred times an hour (flipping a coin isn’t exactly hard) and you’d make a nice tidy salary. But you’re not going to get very rich very fast that way. So let’s see what happens if you try to maximize your expectation. The math says that for every additional dollar you bet, your expectation would go up by $0.50. So the highest expectation would be to bet all $100. Problem solved!
Wait, not so fast. There’s something wrong with betting the whole $100. If you lose, you can’t bet any more. In other words, there’s an opportunity cost to betting too much. If you bet all $100 and lose, you didn’t just lose $100. You lose access to this man and his fabulous bet. And as I’ll convince you in a bit, that access is much more valuable than you might think.
What we’re run into here is a difference between additive and multiplicative finance. Expectation math is additive. But this bet is multiplicative because it’s repeated. If we win, we can come back and bet more the second time. If we lose, we have less to bet with. The effect of this multiplicative aspect to the bet is that large bets (and thus potential large losses) are penalized more than they are in additive finance. We saw that when we looked at the effect of betting the full $100. The question then becomes how much to bet. If $1 is too little and $100 is too much, there has to be some good point in the middle. But where is it? In order to answer that, we need the equivalent of expectation math, but for multiplicative finance.
First though, I hope you see the importance of this thought experiment. It’s intended to be at some level a simulation of your financial life. Over time you’re presented with financial opportunities – opportunities to bet. You can outright discard the ones with negative expectation. But for the positive expectation ones, you have to consider how much to bet. If you underbet, you make very little money like the guy who only bets $1 every time. If you overbet, you can go broke and then make very little money. Somewhere in the middle is a happy medium. You might think that people would naturally gravitate to that value when risking their money, but that turns out to be false.
John Kelly ingeniously solved exactly this problem of multiplicative bets, which is why he gets his face on the poster. The math I’m about to take you through comes from him and from Ed Thorp. This is one of those cases where you just have to man (or woman) up and teach yourself the math. If you don’t understand it fully, there’s a potential for expensive and stupid mistakes. Kelly had three insights:
- That this math should be done in terms of net worth, rather than dollars won or lost.
- The bets are symmetrical with respect to your net worth If you have $100 and bet $10, that’s the same as having $200 and betting $20. So while the amount you bet will change over time, the fraction of your net worth you bet will stay constant as long as the terms of the bet stay constant.
- You should be optimizing for the growth rate of your wealth rather than additive expectation.
- define your net worth to be 1 (in arbitrary units) for convenience
- define X as the amount you lose if you lose the bet, 0 < X < 1
- define Z as the payout when you win Z = 2X in our example
- define P as the probability you win your bet (0.5 or 50% in our example)
- define Q as the probability you lose your bet. P = 1- Q (0.5 our example)
- your expectation E after the bet is thus E = p*(1+Z)+q*(1-X)
- for our example: E = 0.5*(1+2X)+0.5*(1+-X) = 1 + 0.5*X
- This is the same result we got above which is good. But we really care about growth rate, not expectation.
- Here’s where the math gets gnarly: we want to maximize multiplicative growth rate. Multiplying numbers is the same as taking their logarithm to any base of your choice, adding the logs, and then exponentiating back. This means you can take “multiplicative averages” as follows:
- mult_average = p * log( 1-X) + q * log(1+Z)
- the result is the average growth rate in log space. So if you used a base 10 log, it would be the faction of a 10x growth in your wealth that one bet achieves.
- substitute for our example: mult_average = 0.5*log(1+2X)+0.5*log(1-X)
- Now you can take the resulting formula and maximize it. You could do this via calculus (differentiate, take the roots of the derivative, and check for maxes). Or you could get some help from Wolfram Alpha. Feed it:
- The result:
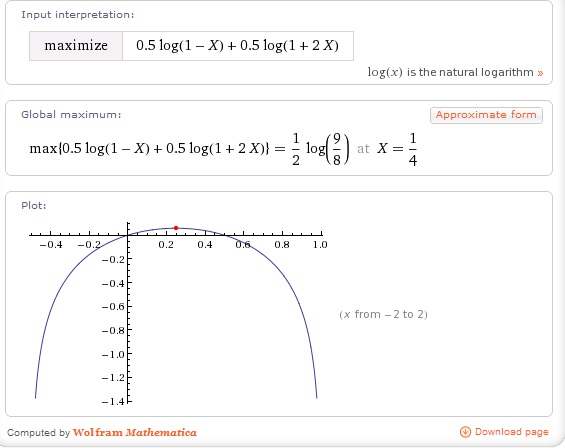
There’s several things to note about this result. First off, it says for our example bet you should wager 1/4 of your bankroll each time. That fits intuition – we knew the answer was somewhere in the middle. Notice how your growth rate approaches zero as the bet goes to zero. No surprise there. Also notice how it approaches zero again at about 50% bet sizing. Past that, it goes infinitely negative. The counter-intuitive result is that if you bet more than half your money each time you will not achieve consistent growth – your growth rate will be zero or negative. You’ll just bounce around at best. This may seem odd since the underlying bet is positive expectation but it’s true. Try it out on paper or in an excel spreadsheet if you don’t believe me.
The power of this sort of exponential growth is immense. If you actually bet at 1/4 bankroll size, each bet would on average increase you net worth by about 6.1%. Bet 100 times per hour, and on average you’d increase your wealth by about 360x per hour. After about an hour and a half, you’d be a millionaire. I’ve written before about the power of repeatedly applying small edges, but I just can’t emphasize it enough.
You should spend some time with the Kelly math. Read the Wikipedia article and make sure you understand it – they presented the same material I did but with a different approach. Check my math and make sure you get the same result. Basically, dive in and become fluent in this stuff.
There’s a lot more to come on this topic – especially the “reduce your bet by 5x” part.
Oh, and on a totally unrated topic the Oakland Athletics just clinched the AL West a few days ago despite having the second lowest payroll in major league baseball. The second place team in their division, the Texas Rangers, spent more than twice as much as the Athletics did. You have to go four notches up the salary ladder from the Athletics to find another team that broke .500 (the Rays) and nine steps up to find another division winner (the Nationals), And how did Billy Beane manage to do the near-impossible yet again? I think it had something to do with math 😉
Interesting way to look at investing. A lot of people might have trouble working through the math but would agree with common-sense rules pretty similar to this. Doesn’t it all come down to controlling volatility/risk? Optimizing growth rate rather than expected value seems to be pointing in the same direction as reducing your bet size. After all an expected value of +$50 on a net worth of $100 is a pretty good growth rate. The only problem is that you run the risk of being out in one bet (which isn’t exactly accurate since you need to invest in the mob to run the risk of permanently losing your future human capital).
So in other words the rule would be to maximize your growth rate while controlling risks of a major setback. I guess the part where people don’t intuitively understand the math is when it comes to the result of slipping one little 0 into a long series of multiplications 🙂
I know it is not the point of the post (and I am positive I missed the point as the math was WAY over my head)…but why not scale back your dream of a proprietary trading firm and get an investment club going?
W,
This is right enough, but your definition of “multiplicative average” is too mysterious and an informal derivation is easy enough. Hopefully your readers would understand that, after N plays, where you’ve won W times and lost L times, your total wealth would be V = (1-X)^L*(1+2*X)^W, where X is the (constant) fraction of your net worth you bet each time. That is really what you want to maximize, but that’s hard because of the exponents. So we use the properties of logarithms and the handy fact that maximizing log V also maximizes V to get log V = L*log(1-X)+W*log(1+2X). Well, that’s easier, but what are L and W? So now instead of maximizing log V, we maximize (log V)/N = L/N*log(1-X)+W/N*log(1+2X) by the same principle. Now we can interpret L/N and W/N as P and Q (in the long run, of course), and we get the same answer.
Like I said, there’s nothing _wrong_ with this post, but I think you do your readers a disservice by eliding over the relatively simple guts of the derivation: as a mathematically sophisticated (okay, maybe not that sophisticated) reader, I was left a bit befuddled by the leap from expected value to your multiplicative average; I can only imagine it being worse for someone for whom logs are unfamiliar. Anyways, those are my two cents. I like your blog, but I’ll start taking you to task when you get sloppy. 🙂
-P
The difficulty here is that there’s no good terminology for what we’re trying to do. You could call it a “weighted geometric mean” instead of a “multiplicative average” if you wanted to put it in dollars scale instead of log-dollars scale. Of course, that gets us no closer to trying to compute the thing. I guess you could go with Wikipedia’s “The log of the geometric mean is the arithmetic mean of the logs of the numbers” as an explanation. But that still doesn’t explicitly tell you how to weight them.
For better or worse, this part of arithmetic is just a terminology sinkhole. I’m not sure the way I approached it was good though. Your derivation looks fine as well, although I think it becomes more awkward than mine when you have more than two outcomes. That’s something we’ll need for some of the advanced applications.